The eight queens problem

The eight queens problem

My program 8QUEENS.PRG included with SIM41.ZIP allows to find all positions for eight queens over a chessboard where nothing queen can capture another.

Example:

In order to describe each position I used a eight digits number where the first digit is the position of the first queen within the first chessboard column, the second digit is the position of the second queen within the second column, and so on until the eight column.

The preceding position, for example, is 15863724.

The one in the first digit means that the queen of the first column is positioned over the first row , the five in the second digit means that the queen of the second column is positioned over the fifth row counting from up to down. The eight in the third digit means that the third queen is positioned over the eight row, and so on until the eight digit.

The program can begins the search from a partial initial position. For Example: 135

If you don't give this data , the program begins puting the first queen over the first upper row of the first column. The other queens are out of the board at the beginning and enter to the board from left to right, each queen searching in her assigned column a row where can not capture to the preceding queens.

If is not possible to put a queen over a row in her assigned column, the queen does not enter to the board and the program moves the queen in the preceding left column to the following row down where the preceding queen will can not capture the other queens at her left and again the program try to put a queen in the current column.

If it's successfull the program try to put a new queen in the following right column. If the program reachs the eight column and achieves to put a queen in that column , the position is shown on the calculator display.

Example: Search positions from partial initial position = 158

1) Execute sim41.exe

Calculator Keyboard      PC Keyboard                     Display
-------------------      -----------                     -------

[XEQ]8QUEENS             [K]8QUEENS[PC_ENTER_KEY]        XEQ 8QUEENS
                                                         PUBLISH?
YES[R/S]                 YES[!]  (Run in Alpha mode is !)
                                                         INITIAL POSITION?
158[R/S]                 158[R]  (Run in normal mode is R)

  .....Wait a few seconds while the calculator searchs for the position.....

                                                         CODES:11432133
(My own codes for catalog the position's point of view.
I will explain it later)

[R/S]                    [R]
                                                         POSITION1=15863724
[R/S]                    [R]        
                                                         ROTATION?
NO[R/S]                  NO[!]
(The position can be viewed from several view points if you answer YES.
I will explain it later)

...... Wait a few seconds while the calculator searchs for a new position ...

                                                         CODES:11432133
(The same point of view for a different position)

[R/S]                    [R]
                                                         POSITION2=16837425
[R/S]                    [R] 
                                                         ROTATION?
NO[R/S]                  NO[!]

...... Wait a few seconds while the calculator searchs for a new position ...


                                                         CODES:11432133
[R/S]                    [R]
                                                         POSITION3=17468253
[R/S]                    [R] 
                                                         ROTATION?
NO[R/S]                  NO[!]

...... Wait a few seconds while the calculator searchs for a new position ...

and so on.

Each position can be seen from four viewpoints: From the chessboard left side, right side, from up side or from down side. I assume that the default side for view and annotate the position is from downside.

For example, the position 15863724 can be viewed and annotated in the following manner:

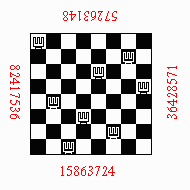
In the chessboard there are several simmetry axis:

You can use translations around the horizontal and vertical simmetry axis for generate new positions from someone position. Also you can apply double translations: first around the vertical axis and later around the horizontal axis.

The double translation first around the vertical axis and later around the horizontal axis is equivalent to the double translation first around the horizontal axis and later around the vertical axis.

Then, each chessboard position generates four positions depending the viewpoint, other four positions if we make a translation around the horizontal axis, other four positions if we make a translation around the vertical axis and other four positions if we use a double translation.

Example: The initial position 15863724 generates the following positions:

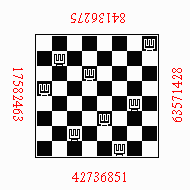
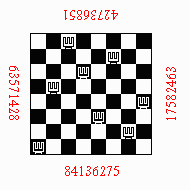
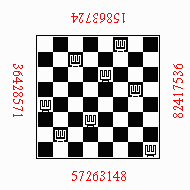
Without rotations: 15863724, 36428571, 57263148, 82417536
With a rotation around the horizontal axis: 84136275, 17582463, 42736851, 63571428
With a rotation around the vertical axis: 42736851, 63571428, 84136275,17582463
With double rotation around both axis: 57263148, 82417536, 15863724, 36428571

Note: I am assigning equal meaning to the words translation and rotation.

Theoretically each position generates sixteen positions but if you look at the positions generated, each position is repeated two times. Then , each position only produces eight positions: The original position and other seven new positions.

One exception: There is one position with complete simmetry with reference to the central point of the chessboard. This position only generates three new positions. Try to find it using the program.

It's possible to find 92 different positions in a 8x8 chessboard

There are 11 independent positions that generate seven new positions and one independent position that generates only three new positions. (11*8+1*4 = 92 )

If you answer YES to the question ROTATION? in the program, the seven new positions associated with the current position are shown.
I assigned the code 11 to the original position viewed from downside, code 12 to the original position viewed from right side, code 13 to the original position viewed from up side and code 14 to the original position viewed from leftside.
The code 21 is the original position rotated around the horizontal axis and viewed from downside, 22 is the same position viewed from right side, 23 is the position viewed from upside and 24 means viewed from left side.
Code 31 means the original position rotated around the vertical axis and viewed from downside, codes 32, 33 and 34 mean this position viewed from leftside, upside and rightside respectively.
Codes 41, 42 , 43 and 44 mean the original position rotated around both axis and viewed from downside, leftside, upside and rightside respectively.
If you wish to find all positions it's enough that the queen in the first column will be put in the range from file 1 to file 4 because the positions obtained with the first queen in files 5 to 8 can be reached with a rotation around the horizontal axis.
The 8QUEENS program obtained 46 positions with the first queen varying from file 1 to file 4.
I named the "Associated position" to the position generated by rotating the original obtained position around the horizontal axis. The 8QUEENS program shows codes as four pairs of two digits numbers. The first two pairs correspond to two viewpoints in the original position and the last two pairs correspond to two viewpoints in the associated position.
Example: For the position: 15863724, CODES=11432133 mean that the original position can be viewed from viewpoint 11 and viewpoint 43 and the associated position 84136275 generates 15863724 from viewpoint 21 and viewpoint 33.

Return to main page